這是以 Claude 輔助撰寫筆記的第二次嘗試(上次是 隨機森林 Random Forest & 表格模型,兩個版本都失敗,結果是 Claude 充份發揮了它的想像力),表現好一些。之後會在時間許可時,逐步修改加入我想放的資料。
我心目中理想的 Claude 輔助撰寫筆記是這樣:Claude 扮演大部分打字和整理的工作,我則接手修飾(因為 GAI 大多廢話贅詞很多)和撰寫真正的感想,而不是我之前形容的,心得分享變成了課程英翻中。
例如 mini-batch 的真實意義:
這堂課的前面,Jeremy 老師還在補充前一個主題,後面則在抒發心得(因為是第一階段的最後一堂課),所以真正講述的內容不多。
主要就講解 CNN 的概念,並以一個試算表補充。所以筆記會以書上的資料(第13章)為主。
CNN 的概念,推薦李弘毅老師的講解,淺顯易懂,連結(包含 影片和 議義)放在參考資料中。
Convolution(卷積) = con-(一起) + volv-(滾動、捲曲)+ -tion(名詞化)
字面意思:「一起滾動或捲起來的過程」,即「盤繞、纏繞」的概念。
一種數學運算,合併兩個函數、產生一個新的函數,表達其相互影響。
▌卷積的基本概念
特徵工程簡介
在機器學習領域,特徵工程(Feature engineering)是指將原始數據轉換為更適合模型的形式。對於圖像來說,特徵可以是視覺上的獨特屬性,如邊緣、紋理或形狀等。
術語解釋:特徵工程指創建輸入數據的新轉換,使其更易於建模。
將原始資料轉換成更能表達與任務相關模式的形式。
例如本範例中的直線、橫線、斜線所組合而成的數字 0~9。
或是信用卡盜刷中的日期格式。以特徵工程將時間戳轉換為以下特徵:距離上次交易間隔時間(頻率突然提高)、刷卡時間是否為正常交易時段(半夜兩三點)。
以數字識別為例:
- 數字「7」的特徵:頂部的水平邊緣和從右上到左下的對角線邊緣
- 數字「3」的特徵:不同方向的對角線和水平邊緣
如果我們能夠提取圖像中邊緣出現的位置信息,並用這些信息作為特徵,而不是原始像素值,可能會得到更好的結果。這正是卷積(Convolution)所做的工作。
卷積基礎
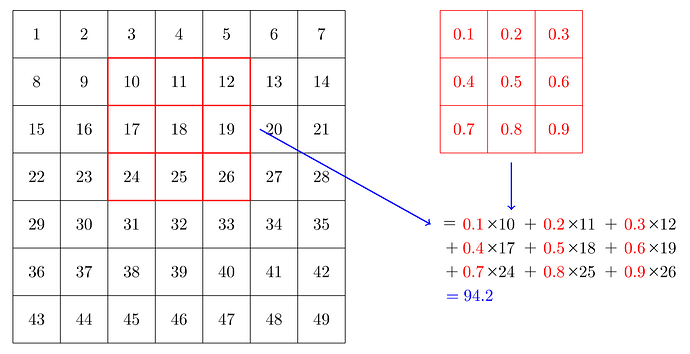
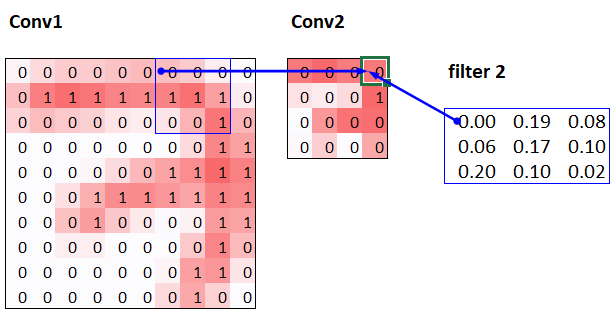
卷積是一種基本的數學運算,僅需乘法和加法,就能實現圖像特徵提取。卷積需要一個卷積核(kernel),也稱為濾波器,通常是一個小矩陣(如3×3)。
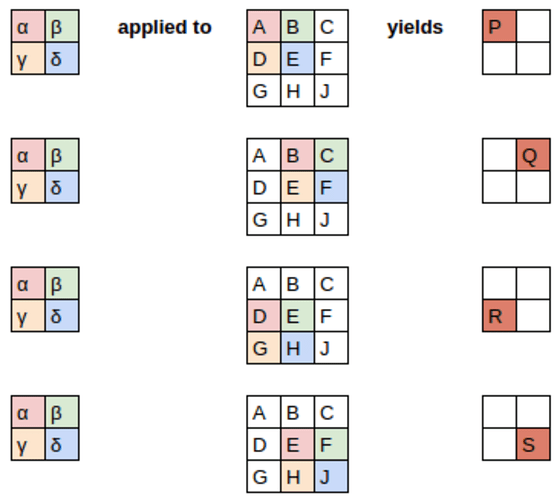
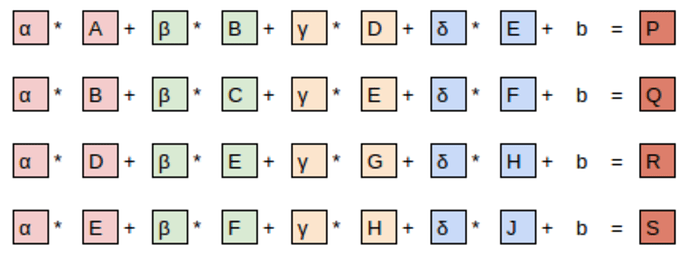
卷積操作示例:
- 將卷積核應用於圖像的一個小區域(比如3×3的塊)
- 對應元素相乘
- 將乘積相加得到一個輸出值
邊緣檢測實例
讓我們通過程式碼實例了解卷積如何檢測邊緣:
# 頂部邊緣檢測卷積核
top_edge = tensor([[-1,-1,-1],
[ 0, 0, 0],
[ 1, 1, 1]]).float()
這個卷積核設計用於檢測水平邊緣,特別是從暗到亮的過渡(從上到下)。當應用於有暗色上方區域和亮色下方區域的圖像時,會產生較強的正值響應。
應用於圖像時,計算過程如下:
# 在圖像的小區域應用卷積核
im3_t[0:3,0:3] * top_edge
# 計算結果總和
(im3_t[0:3,0:3] * top_edge).sum()
卷積核的數學原理:若使用上述頂部邊緣卷積核,對於像素值為 a1~a9 的3×3區域(按左上到右下排序),卷積結果為:
結果 = -a1 - a2 - a3 + a7 + a8 + a9
這意味著:
- 當上方區域(a1,a2,a3)暗(值小)且下方區域(a7,a8,a9)亮(值大)時,結果為較大的正值
- 當上方區域亮且下方區域暗時,結果為較大的負值
- 當上下區域亮度相似時,結果接近零
通過這種方式,卷積核有效地檢測出從暗到亮的水平邊緣。
▌卷積數學原理
卷積映射
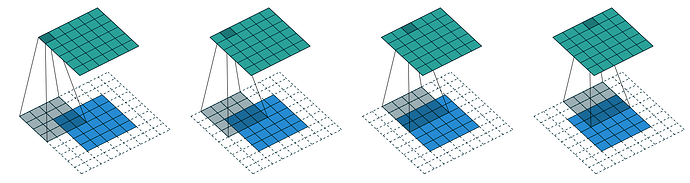
將卷積核應用於整個圖像需要在每個可能的位置進行計算。對於一個h×w的圖像和一個k×k的卷積核(不考慮填充),輸出將是(h-k+1)×(w-k+1)大小的特徵圖。
下面的程式碼演示了如何實現這一過程:
# 定義一個應用卷積核的函數
def apply_kernel(row, col, kernel):
return (im3_t[row-1:row+2,col-1:col+2] * kernel).sum()
# 在整個坐標網格上應用卷積核
rng = range(1,27)
top_edge3 = tensor([[apply_kernel(i,j,top_edge) for j in rng] for i in rng])
我們可以創建不同類型的卷積核來檢測不同特徵:
- 水平邊緣檢測器(檢測從暗到亮或從亮到暗的水平過渡)
- 垂直邊緣檢測器(例如:
left_edge = tensor([[-1,0,1],[-1,0,1],[-1,0,1]])檢測從左到右的暗到亮過渡) - 對角線邊緣檢測器
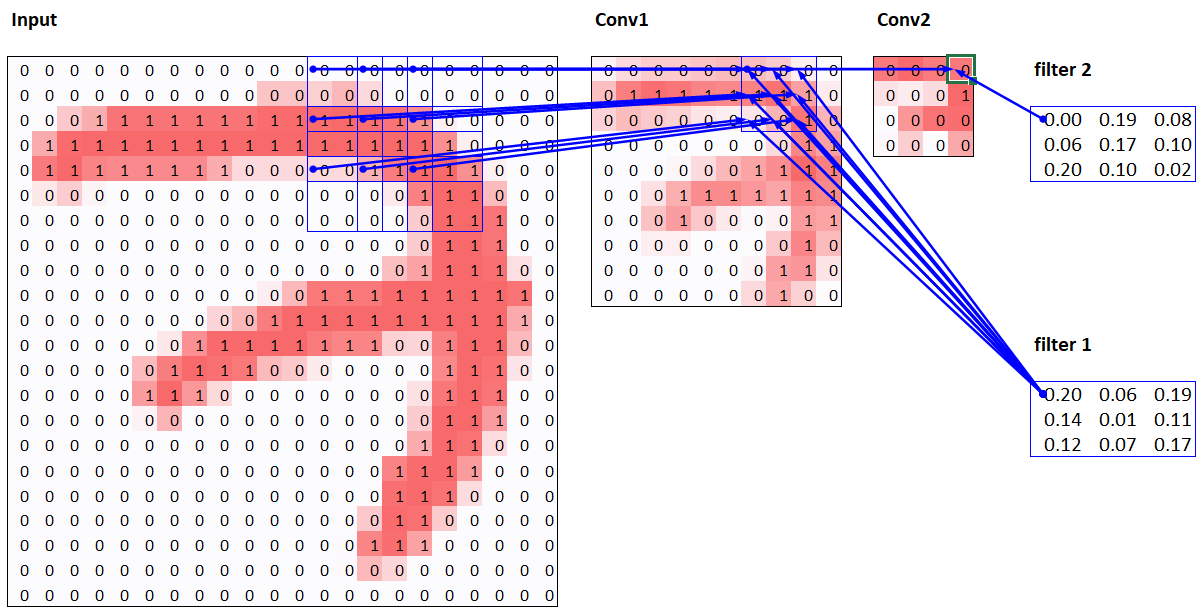
通過這些不同的卷積核,我們可以提取圖像中的各種特徵,這些特徵對於識別和分類任務非常有用。

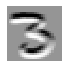

▌PyTorch中的卷積
PyTorch提供了高效的卷積實現:F.conv2d,其主要參數包括:
input: 形狀為(minibatch, in_channels, iH, iW)的輸入張量weight: 形狀為(out_channels, in_channels, kH, kW)的濾波器
PyTorch的卷積具有幾個強大特性:
- 可以同時對批次中的多張圖像應用卷積
- 可以同時應用多個卷積核
- 可以利用GPU並行處理,大幅提升速度
示例:
# 創建多個邊緣檢測卷積核
edge_kernels = torch.stack([left_edge, top_edge, diag1_edge, diag2_edge])
# 調整形狀以符合PyTorch期望的輸入(增加輸入通道維度)
edge_kernels = edge_kernels.unsqueeze(1)
# 應用卷積
batch_features = F.conv2d(xb, edge_kernels)
在這個例子中,我們將四種不同的邊緣檢測器應用於輸入圖像,每種檢測器會產生自己的特徵圖。PyTorch的實現允許我們一次性執行所有這些操作,大大提高了效率。
▌步幅與填充
填充(Padding)
當應用卷積操作時,輸出特徵圖的大小會小於原始圖像。為了保持輸出大小與輸入相同,我們可以在圖像周圍添加額外的像素,稱為填充(通常是填充零)。
對於大小為 ks × ks 的卷積核(ks 為奇數),需要 ks//2 的填充才能保持輸出大小與輸入相同。例如,3×3的卷積核需要1個像素的填充,5×5的卷積核需要2個像素的填充。
步幅(Stride)
步幅定義了卷積核在圖像上移動的像素數。默認步幅為1,但我們也可以使用更大的步幅:
- 步幅1:每次移動1個像素,輸出特徵圖與輸入大小相近(取決於填充)
- 步幅2:每次移動2個像素,輸出特徵圖的寬高約為輸入的一半
- 更大步幅可以進一步減小輸出特徵圖的大小
使用填充為1和步幅為2的情況下,h×w大小的圖像將產生大約(h+1)//2 × (w+1)//2大小的輸出。一般公式為:(n + 2*pad - ks)//stride + 1,其中n是輸入維度,pad是填充大小,ks是卷積核大小,stride是步幅。
這些參數的選擇對網絡架構設計至關重要:
- 步幅1的卷積通常用於保持特徵圖大小不變,同時處理特徵
- 步幅2的卷積用於下採樣,減小特徵圖大小並增加感受野
▌卷積方程理解
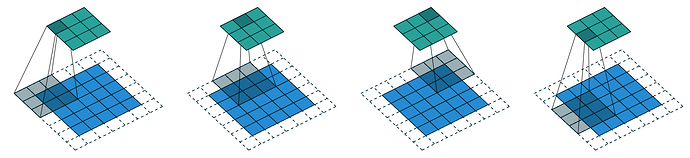
卷積可以從多個視角理解:
-
直觀理解:將卷積核逐一應用於圖像的每個位置,計算加權和
-
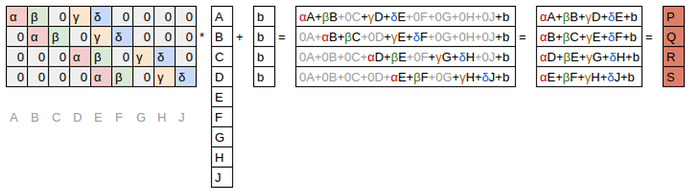
矩陣運算視角:卷積可以表示為特殊的矩陣乘法,其中:
- 權重矩陣中有固定的零元素(灰色顯示)
- 某些權重是共享的(必須保持相等)
這種權重共享和稀疏連接的特性使卷積網絡參數更少,但仍能表示複雜的視覺特徵。卷積層的這些約束實際上是一種有效的歸納偏置(inductive bias),特別適合處理具有空間結構的數據,如圖像。
▌構建第一個CNN
我們不必手動設計卷積核,而是可以通過隨機梯度下降(SGD)學習它們的值。使用卷積層替代或配合常規線性層,我們創建了卷積神經網絡(CNN)。
基本CNN架構
從簡單的線性網絡開始:
simple_net = nn.Sequential(
nn.Linear(28*28,30),
nn.ReLU(),
nn.Linear(30,1)
)
轉換為卷積架構:
# 定義卷積模塊
def conv(ni, nf, ks=3, act=True):
res = nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)
if act: res = nn.Sequential(res, nn.ReLU())
return res
# 構建簡單CNN
simple_cnn = sequential(
conv(1 ,4), #14x14
conv(4 ,8), #7x7
conv(8 ,16), #4x4
conv(16,32), #2x2
conv(32,2, act=False), #1x1
Flatten(),
)
與線性層不同,卷積層不需要指定輸入大小,因為卷積自動應用於每個像素。步幅為2的卷積會將特徵圖大小減半,通常我們會同時增加通道數以保持網絡容量。
這裡的關鍵設計原則是:
- 使用步幅2的卷積減小特徵圖大小
- 隨著特徵圖尺寸減小,增加通道數(特徵數)
- 最後使用
Flatten()將最終的特徵圖轉換為向量,用於分類
網絡訓練
learn = Learner(dls, simple_cnn, loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(2, 0.01)
透過訓練,網絡會自動學習有用的特徵卷積核,這些特徵對於識別任務是最有用的。這比手動設計特徵提取器更有效,因為網絡可以根據數據自適應地學習最相關的特徵。
▌感受野
感受野是指影響一個層中特定位置輸出的輸入區域。深層網絡的感受野會隨著層數增加而擴大,特別是使用步幅大於1的卷積時。
例如,對於兩個連續的步幅為2的卷積層:
- 第一層的每個輸出受到原始圖像中3×3區域的影響
- 第二層的每個輸出受到原始圖像中7×7區域的影響
這可以通過跟踪計算路徑來理解:第二層的一個單元依賴於第一層的3×3區域,而第一層的每個單元又依賴於原始圖像的3×3區域,綜合起來就是7×7的感受野。
隨著網絡深度增加,感受野擴大,網絡可以學習更複雜的特徵。這就是為什麼深層網絡中通常會增加通道數的原因之一 — 處理更大感受野的複雜特徵需要更多的參數。
▌彩色圖像處理
彩色圖像是一個三維張量,第一個維度包含顏色通道(紅、綠、藍):
im = image2tensor(Image.open(image_bear()))
im.shape # torch.Size([3, 1000, 846])
對於彩色圖像的卷積,卷積核需要匹配輸入通道數:
- 對於RGB圖像,第一層的卷積核形狀為[輸出通道數, 3, 核高, 核寬]
- 每個輸入通道都有自己的濾波器
卷積運算會在所有通道上進行,然後將結果加總,產生一個數值,即特徵圖中單個位置的激活值。數學上表示為:
輸出(i,j) = 偏置 +
∑(輸入通道c)
∑(核高h)
∑(核寬w)
卷積核(c,h,w) * 輸入(c, i+h, j+w)
在PyTorch中,卷積權重的維度順序是:[輸出通道, 輸入通道, 核高, 核寬]。例如,對於第一層處理RGB圖像的16個卷積核,權重形狀為[16, 3, 3, 3]。
處理彩色圖像時不需要特別的機制,只需確保第一層有正確數量的輸入通道(RGB為3)。
▌提升訓練穩定性
在訓練深度網絡時,我們常常面臨不穩定性問題。以下是一些改進策略:
1. 增加批次大小
較大的批次提供更準確的梯度,但會減少每個周期的更新次數:
dls = get_dls(512) # 增加批次大小至512
優點:
- 梯度更穩定,減少隨機性
- 可以使用更高的學習率
缺點:
- 每個周期的更新次數減少
- 可能會在某些情況下泛化性能略差
- 需要更多的GPU記憶體
2. 1cycle訓練
Leslie Smith提出的1cycle訓練方法包括:
- 從低學習率開始,逐漸增加到高學習率(預熱階段)
- 然後再逐漸降低回低學習率(退火階段)
這種方法允許我們使用更高的最大學習率,帶來兩個主要好處:
- 更快的訓練速度(超收斂現象)
- 更好的泛化性能(避免陷入尖銳的局部最小值)
在fastai中使用1cycle訓練:
learn.fit_one_cycle(epochs, lr)
動量(momentum)也會循環變化,與學習率方向相反:高學習率時使用較低動量,退火階段使用較高動量。這種策略進一步增強了訓練的穩定性。
原理上,高學習率有助於跳出尖銳的局部最小值,而最終的低學習率階段則幫助模型精確收斂到一個良好的最小值。
▌批次正規化
批次正規化(Batch Normalization)是解決訓練不穩定和激活接近零問題的有效方法。Sergey Ioffe和Christian Szegedy在2015年提出,可以:
- 加速深度網絡訓練
- 使用更高的學習率
- 對初始化不那麼敏感
- 改善模型泛化能力
工作原理
批次正規化通過計算層激活的平均值和標準差,並用這些統計量來正規化激活。對於輸入 x,批次正規化的基本公式為:
y = γ * (x - μ)/σ + β
其中:
- μ 是批次的平均值
- σ 是批次的標準差
- γ 和 β 是可學習的縮放和偏移參數
α (Alpha)
β (Beta)
γ (Gamma)
δ (Delta)Batch Normalization 對每一層的輸入進行標準化,使其近似均值為 0、標準差為 1,然後通過可學習的參數 γ 和 β 進行縮放和偏移,減少內部協變量偏移(internal covariate shift),提高學習速度與穩定性。
主要差異:
- 位置:批次正規化通常應用於層的輸入,而不是輸出(雖然從數學上講,它可以被視為前一層的輸出處理)
- 完整過程:批次正規化不僅進行標準化,還有後續的縮放和偏移步驟:
- 首先標準化:(x - μ)/σ
- 然後縮放和偏移:γ * (標準化結果) + β
- 其中 γ 和 β 是可學習的參數
- 目的:批次正規化的主要目的是減少「內部協變量偏移」,即深度網絡中每層輸入分佈的變化
這個過程使網絡能夠使用更高的學習率、不那麼依賴精確的初始化,並且在訓練過程中保持更穩定的激活分佈。
這些可學習參數使網絡能夠恢復原始的表達能力,同時保持正規化的優勢。
# 在卷積函數中加入批次正規化
def conv(ni, nf, ks=3, act=True):
layers = [nn.Conv2d(ni, nf, stride=2, kernel_size=ks, padding=ks//2)]
if act: layers.append(nn.ReLU())
layers.append(nn.BatchNorm2d(nf))
return nn.Sequential(*layers)
批次正規化的行為在訓練和驗證階段不同:
- 訓練時:使用當前批次的統計量來正規化
- 驗證時:使用訓練期間計算的統計量的運行平均值
泛化效果
含有批次正規化層的模型往往泛化性能更好,主要原因是:
- 批次正規化為訓練過程增加了隨機性(每個批次的統計量略有不同)
- 模型必須學會對這些變化保持穩健
- 這種隨機性有類似正則化的效果,有助於減少過擬合
批次正規化顯著改善了訓練穩定性,使我們能夠使用更高的學習率並獲得更好的準確率。在大多數現代卷積網絡中,批次正規化(或其變體)都是標準組件。
▌總結與實踐建議
-
卷積基礎
- 卷積是一種特殊的矩陣乘法,具有稀疏連接和權重共享特性
- 這些約束使模型參數更少,同時保留表示複雜視覺特徵的能力
- 卷積核可以學習檢測各種特徵,從簡單的邊緣到複雜的模式
-
CNN架構設計
- 使用步幅2的卷積減小特徵圖大小
- 在減小特徵圖大小的同時增加通道數
- 在第一層使用較大的卷積核(如5×5)以獲取更多信息
- 設計網絡時考慮感受野的大小和計算複雜度的平衡
-
訓練技巧
- 使用批次正規化提高訓練穩定性
- 採用1cycle學習率調度
- 監控層激活分布,避免大量近零激活
- 根據需要調整批次大小以平衡穩定性和更新頻率
-
實用指南
- 圖像分類通常使用卷積層提取特徵,然後用全連接層進行分類
- 批次正規化通常放在非線性激活函數之前
- 使用可視化工具(如激活統計和色彩維度圖)診斷訓練問題
通過這些技術和理解,我們可以構建高效、穩定的卷積神經網絡,用於各種計算機視覺任務。CNN已成為現代計算機視覺的基石,從簡單的分類任務到複雜的目標檢測和語義分割,都離不開卷積的基本原理。
▌參考資料
推薦影片
李弘毅老師的 CNN 課程。2021年錄製,至今依然是我看過最棒的影片。
老師影片中使用的 簡報檔。
3Blue1Brown 關於 Neural networks 的系列影片。3Blue1Brown 是我看過視覺化教學最棒的 YouTuber,這系列也不例外。他的強項是以影像表現數學概念,在微積分和線性代數的表現特別突出。這系列影片我的收穫依然很多,但可能程度未到,還是有些地方不太理解。
系列影片有 8 部,並非同時期錄製。CNN主題我推薦至少看前兩部,有空的話再加兩部,會了解的更透徹。
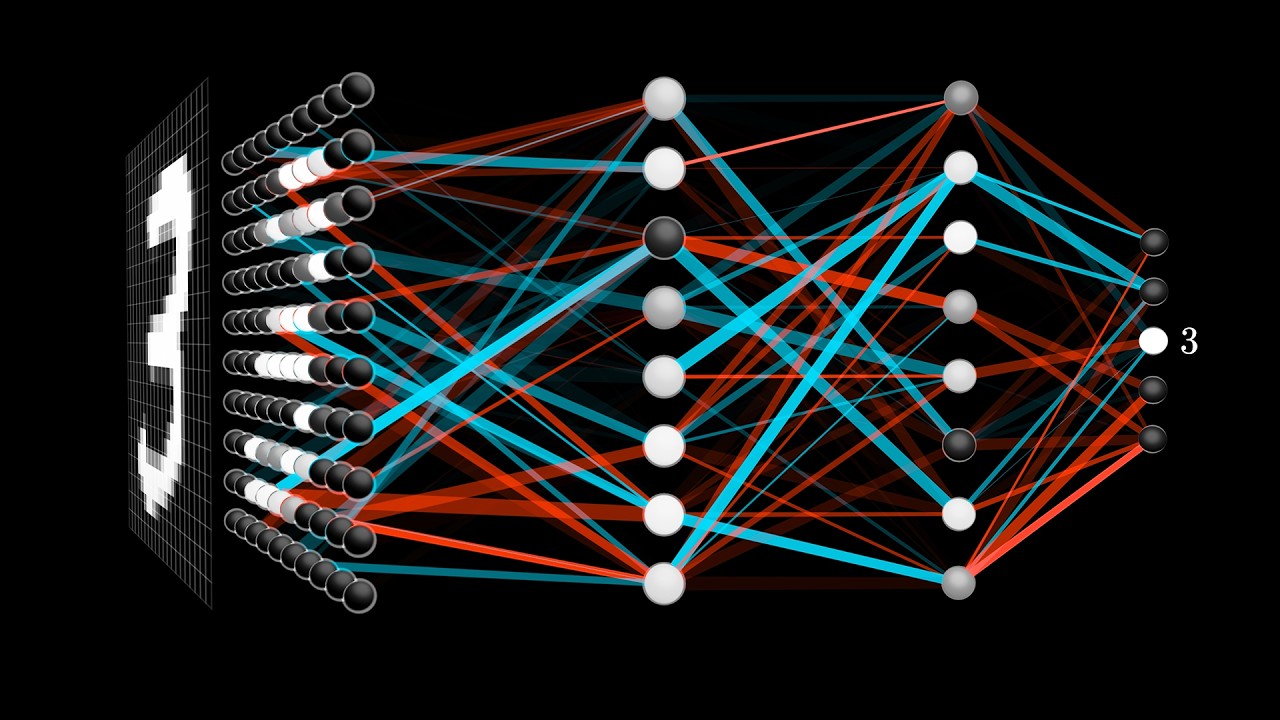
權重(weight)告訴我們下一層的神經元所關注的圖樣。
偏置(bias)則告訴我們加權總和要超過什麼程度才是有意義的。
術語對照表
| 英文 | 繁體中文 |
|---|---|
| Convolution | 卷積 |
| Kernel/Filter | 卷積核/濾波器 |
| Feature | 特徵 |
| Feature engineering | 特徵工程 |
| Edge detector | 邊緣檢測器 |
| Padding | 填充 |
| Stride | 步幅 |
| Channel | 通道 |
| Activation map/Feature map | 激活圖/特徵圖 |
| Receptive field | 感受野 |
| Batch normalization | 批次正規化 |
| 1cycle training | 1cycle訓練 |
| Learning rate | 學習率 |
| Momentum | 動量 |
| Weight sharing | 權重共享 |
| Inductive bias | 歸納偏置 |
| Spatial structure | 空間結構 |
常見問題解答
-
問:為什麼使用卷積而不是全連接層處理圖像?
答:卷積利用權重共享和局部連接,大大減少參數數量,更適合處理圖像的空間結構。對於28×28的圖像,全連接層需要784個輸入參數,而3×3卷積核只需要9個參數。 -
問:如何選擇卷積核大小?
答:通常使用3×3或5×5,較小的核速度更快,較大的核可以捕獲更大範圍的特徵。第一層常用較大的卷積核(5×5),以捕獲更多原始信息。 -
問:為什麼在步幅2的卷積後增加通道數?
答:步幅2將特徵圖面積減少4倍,增加通道數可以維持網絡容量和表達能力。此外,更深的層需要表示更複雜的特徵,因此需要更多的通道。 -
問:批次正規化和層正規化有什麼區別?
答:批次正規化在批次維度上正規化,層正規化在特徵維度上正規化。批次正規化在小批次時效果可能下降,而層正規化不受批次大小影響。 -
問:如何避免訓練過程中的不穩定性?
答:使用批次正規化、適當的學習率調度(如1cycle)、監控層激活分布,避免權重初始化不當。確保網絡中沒有大量接近零的激活,這會導致梯度問題。
習題解答
書中所有的 40 個問題,一樣請 Claude 代為解惑: Lesson 8. 卷積神經網絡(CNN)習題解答 。