110 學年度指定科目考試試題:數學甲
第壹部分:選擇題(單選題、多選題及選填題共占 76 分)
一、單選題(占 18 分)
說明:第 1 題至第 3 題,每題有 5 個選項,其中只有一個是正確或最適當的選項,請劃記在答案卡之「選擇(填)題答案區」。各題答對者,得 6 分;答錯、未作答或劃記多於一個選項者,該題以零分計算。
1.設 x_0、y_0 為正實數。若坐標平面上的點 (10x_0 \ , 100y_0) 在函數 y=10^x 的圖形上,則點 (x_0 \ , \ log y_0) 會在直線 y=ax+b 的圖形上,其中 a、b 為實數。試問 2a−b 的值為何?
(1) \ 4
(2) \ 9
(3) \ 15
(4) \ 18
(5) \ 22
2.研究團隊採用某快篩試劑的檢驗,以了解保護區內生物因環境汙染而導致體內毒素累積超過標準的比率。此試劑檢驗結果只有紅色、黃色兩種。依據過去的經驗得知:若體內毒素累積超過標準,經此試劑檢驗後,有 75\% 顯示為紅色;若體內毒素累積未超過標準,經此試劑檢驗後,有 95\% 顯示為黃色。已知此保護區的某類生物經試劑檢驗後,有 7.8\% 的結果顯示為紅色。假設此類生物實際體內毒素累積超過標準的比率為 p\% ,試選出正確的選項。
(1) \ 1 \le p<3
(2) \ 3 \le p<5
(3) \ 5 \le p<7
(4) \ 7 \le p<9
(5) \ 9 \le p<11
3.試求極限 \ \lim_{n \to \infty} {10^{10} \over n^{10}}[1^9+2^9+3^9+...+(2n)^9] 的值。
(以下這種數學式較美觀,不會被行高約束,但沒找到置左的方法)
(1) \ 10^9
(2) \ 10^9 × (2^{10}-1)
(3) \ 2^9 × (10^{10}-1)
(4) \ 10^9 × 2^{10}
(5) \ 2^9 × 10^{10}
二、多選題(占 40 分)
說明:第 4 題至第 8 題,每題有 5 個選項,其中至少有一個是正確的選項,請將正確選項劃記在答案卡之「選擇(填)題答案區」。各題之選項獨立判定,所有選項均答對者,得 8 分;答錯 1 個選項者,得 4.8 分;答錯 2 個選項者,得 1.6 分;答錯多於 2 個選項或所有選項均未作答者,該題以零分計算。
4.某電子公司有數百名員工,其用餐方式分為自備、外食兩種。經長期調查發現:若當日用餐為自備的員工,則隔天會有 10\% 轉為外食;若當日用餐為外食的員工,則隔天會有 20\% 轉為自備。
假設 x_0、y_0 分別代表該公司今日用餐自備人數與外食人數占員工總人數的比例,其中 x_0、y_0 皆為正數,且 x_n、y_n 分別代表經過 n 日後用餐自備人數與外食人數占員工總人數的比例。在該公司員工不變動的情形下,試選出正確的選項。
(1) \ y_1 = 0.9 \ y_0 + 0.2 \ x_0
(2) \ \begin{bmatrix} x_{n+1} \\ y_{n+1} \end{bmatrix} = \begin{bmatrix} 0.9 & 0.2 \\ 0.1 & 0.8 \end{bmatrix} \begin{bmatrix} x_n \\ y_n \end{bmatrix}
(3) \ 若 {x_0 \over y_0} = {2 \over 1},則 {x_n \over y_n} = {2 \over 1} 對任意正整數 \ n \ 均成立
(4) \ 若 y_0 > x_0,則 y_1 > x_1
(5) \ 若 x_0 > y_0,則 x_0 > x_1
5.假設 f(x) 為五次實係數多項式,且 f(x) 除以 x^n−1 的餘式為 r_n(x) , n 是正整數。
試選出正確的選項。
(1) \ r_1(x)=f(1)
(2) \ r_2(x) \ 是一次實係數多項式
(3) \ r_4(x) \ 除以 \ x^2-1 \ 所得的餘式等於 \ r_2(x)
(4) \ r_5(x) = r_6(x)
(5) \ 若 \ f(-x)=-f(x),則 \ r_3(-x)=-r_3(x)
6.一個標有 1 至 12 號格子的 12 格戳戳樂遊戲,每回遊戲以投擲一枚均勻銅板四次來決定要戳哪些格子。規則如下:
(一)第一次投擲銅板,若是正面,則戳 1 號格子;若是反面,則戳 3 號格子。
(二)第二、三、四次投擲銅板,若是正面,則所戳格子的號碼為前一次所戳格子的號碼加 1 ;若是反面,則所戳格子的號碼為前一次所戳格子的號碼加 3 ,依此類推。
例如:投擲銅板四次的結果依序為「正、反、反、正」,則會戳編號分別為 1、4、7、8 號的四個格子。
假設 p_m 代表在每回遊戲中 m 號格子被戳到的機率,試選出正確的選項。
(1) \ p_2 = {1 \over 4}
(2) \ p_3 = {1 \over 2}
(3) \ p_4 = {1 \over 2}p_1 + {1 \over 2}p_3
(4) \ p_8 > p_{10}
(5) \ 在4號格子被戳到的條件下,3號格子被戳到的機率為 {1 \over 2}
7.設 F(x) 為一實係數多項式且 F'(x)=f(x) 。已知 f'(x)>x^2+1.1 對所有的實數 x 均成立,試選出正確的選項。
(1) \ f'(x) \ 為遞增函數
(2) \ f(x) \ 為遞增函數
(3) \ F(x) \ 為遞增函數
(4) \ [f(x)]^2 \ 為遞增函數
(5) \ f(f(x)) \ 為遞增函數
8.已知 z_1、z_2、z_3、z_4 為四個相異複數,且其在複數平面上所對應的點,依序可連成一個平行四邊形,試問下列哪些選項必為實數?
(1) \ (z_1-z_3)(z_2-z_4)
(2) \ z_1 - z_2 + z_3 - z_4
(3) \ z_1 + z_2 + z_3 + z_4
(4) \ {{z_1 + z_2} \over {z_3 - z_4}}
(5) \ \left( {z_2 - z_4} \over {z_1 - z_3} \right)^{2}
三、選填題(占 18 分)
說明:
1.第 A 至 C 題,將答案劃記在答案卡之「選擇(填)題答案區」所標示的列號(⑨–㉒)。
2.每題完全答對給 6 分,答錯不倒扣,未完全答對不給分。
A.從 6、8、10、12 中任取三個相異數字,作為三角形的三邊長,且設此三角形的最大內角為 θ 。在所有可能構成的三角形中, \cos θ 的最小值為 \underline{{⑨ \ ⑩ \ ⑪} \over {⑫ \ ⑬}} 。
(化成最簡分數)
B.坐標平面上,一個半徑為 12 的圓與直線 x+y=0 相交於兩點,且這兩點的距離為 8 。若此圓與直線 x+y=24 交於 P、Q 兩點,則線段 \overline{PQ} 的長度為 \underline{⑭\sqrt{⑮}} 。
(化成最簡根式)
C.考慮一梯形 ABCD ,其中 \overline{AB} 與 \overline{DC} 平行。已知點 E、F 分別在對角線 \overline{AC}、\overline{BD} 上, \overline{AB}= {2 \over 5}\overline{DC}、\overline{AE}= {3 \over 2}\overline{EC}、\overline{BF}= {2 \over 3}\overline{FD} ,如圖所示。
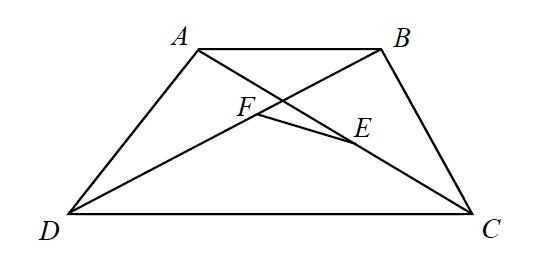
若將向量 \overset{\rightharpoonup }{FE} 表示成 \alpha \overset{\rightharpoonup }{AC} + \beta \overset{\rightharpoonup }{AD} ,則實數 \alpha = \underline{{⑯} \over {⑰ \ ⑱}} \ 、 \ \beta = \underline{{⑲ \ ⑳} \over {㉑ \ ㉒}} 。
(化成最簡分數)
─ ─ ─ 以下是第貳部分的非選擇題,必須在答案卷面作答 ─ ─ ─
第貳部分:非選擇題(占 24 分)
說明:本部分共有二大題,答案必須寫在「答案卷」上,並於題號欄標明大題號(一、二)與子題號((1)、(2)、……),同時必須寫出演算過程或理由,否則將予扣分甚至零分。作答使用筆尖較粗之黑色墨水的筆書寫,且不得使用鉛筆。若因字跡潦草、未標示題號、標錯題號等原因,致評閱人員無法清楚辨識,該部分不予計分。每一子題配分標於題末。
一、坐標空間中,令 E 為通過三點 A(0,−1,−1)、B(1,−1,−2)、C(0,1,0) 的平面。假設 H 為空間中一點,且滿足 \overset{\rightharpoonup}{AH} = {2 \over 3}\overset{\rightharpoonup}{AB} - {1 \over 3}\overset{\rightharpoonup}{AC} + 3(\overset{\rightharpoonup}{AB} × \overset{\rightharpoonup}{AC}) 。根據上述,試回答下列問題。
(1) \ 試求四面體 ABCH 的體積。( 4 分)(註:四面體體積為三分之一的底面積乘以高)
(2) \ 令點 H′ 為點 H 相對於平面 E 的對稱點,試求 H′ 的坐標。( 4 分)
(3) \ 試判斷點 H′ 在平面 E 的投影點是否位在 \Delta ABC 的內部?並說明理由。( 4 分)(註:三角形的內部不含三角形的三邊)
二、坐標平面上,以 \Gamma 表示多項式函數 y=x^3-4x^2+5x 的圖形,且以 L 表示直線 y=mx ,其中 m 為實數。根據上述,試回答下列問題。
(1) \ 當 m=2 時,試求出在 x \ge 0 的範圍內, \Gamma 與 L 的三個相異交點的 x 坐標。( 2 分)
(2) \ 承 (1) ,試求 \Gamma 與 L 所圍有界區域面積的值。( 4 分)
(3) \ 在 x \ge 0 的範圍內,若 \Gamma 與 L 有三個相異交點,則滿足此條件的 m 之最大範圍為 a<m<b ,試求 a、b 之值。( 6 分)
選擇(填)題參考答案
資料來源:大學入學考試中心