Introduction
- 布林值, 0(False), 1(True) | bool
- 整數(Z), Integer Numbers | int
- 有理數(Q), Rational Numbers | fraction.Fraction
- 實數(R), Real Numbers | float/decimal.Decimal
- 複數(C), Complex Numbers | complex
Integers: Data Types
- 僅考慮正數,則 8bit 可用來表示 (0 ~ 255),共 256 個整數
- 若同時考慮正負數,其中一個位元拿去表示正負,而 0 無正負值,可再擠出一個位置 (-128 ~ 127)
- 16 位元(signed)integers → Range [-32,768 ~ 32,767]
- 32 位元(signed)integers → Range [-2,147,483,648 ~ 2,147,483,647]
- 32 位元(unsigned)integers → Range [0 ~ 4,294,967,296]
- JAVA → Byte(8-bit), short(16-bit), int(32-bit), long(64-bit)
- Python → The INT object uses a variable number of bits, and increase the bits dynamically (32, 64, 96 bits … etc.)
- Since INTs are actually objects, there is a further fixed overhead per integer
import sys
print(sys.getsizeof(0)) # an integer object takes at least 24 bytes (Object Overhead)
print(sys.getsizeof(1)) # it takes 24(overhead) + 4 = 28 bytes
print(sys.getsizeof(2**1000)) # it takes 24(overhead) + 136 = 160 bytes
# Python seamlessly dynamically extend the size to accommodate the length of the integer object.
# When the integer gets bigger, it requires more memory for storage and the operation get slower.
28
28
160
import time
def calc(a):
for i in range(10000000):
a * 2
start1 = time.perf_counter()
calc(10) # small integer
end1 = time.perf_counter()
print("It takes :", end1 - start1)
print("_" * 50)
start2 = time.perf_counter()
calc(2**10000) # much much bigger integer
end2 = time.perf_counter()
print("It takes :", end2 - start2)
It takes : 0.8512875000014901
__________________________________________________
It takes : 7.090256199706346
Integers: Operations
- addition(+), subtraction(-), multiplication(*), exponent(**) → return integer
- However, division(/) --> always return float (even the case without remainder)
- There are two more operators for integer →
- // (Floor division - div)
- % (Modulo - mod)
- The floor of a real number a → the largest integer <= a (Floor 的定義: 小於等於 實數 a 的最大整數)
- floor(3.14) → 3
- floor(1.9999) → 1
- floor(2) → 2
- floor(-3.1) → -4 (for negative number, floor is not quite the sams as truncation!)
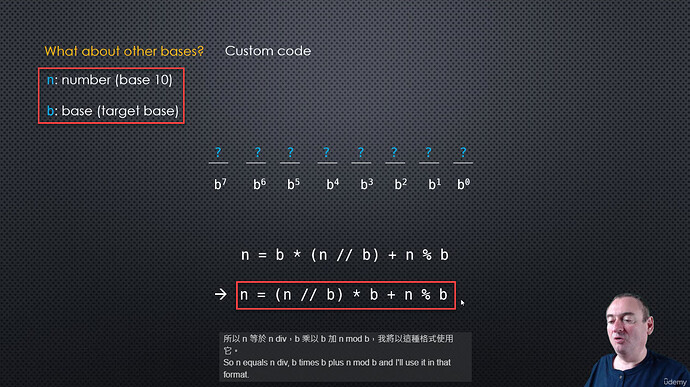
- The equation to satisfy => a = b * (a//b) + a % b
- Example: 155 = 4 * (155 // 4) + (155 % 4) = 4 * 38 + 3
- Mod → is not the remainder, it’s just something that has to satisfy the equation
print(type(1+1))
print(type(4-10))
print(type(2*3))
print(type(2**5))
print("_" * 50)
print(type(2/3)) # float
print(type(10/2), (10/2))
<class 'int'>
<class 'int'>
<class 'int'>
<class 'int'>
__________________________________________________
<class 'float'>
<class 'float'> 5.0
import math
print(math.floor(3.15))
print(float(3.999999999999999))
print(math.floor(3.999999999999999)) # 小數位數 15 => Still 3
print(float(3.9999999999999999))
print(math.floor(3.9999999999999999)) # 4 => floats have a limited precision in Python
print("_" * 50)
print(math.floor(-3.15)) # -4
print(math.floor(-3.000000000000001)) # -4
print(math.floor(-3.0000000000000001)) # -3 => floats have a limited precision in Python
3
3.999999999999999
3
4.0
4
__________________________________________________
-4
-4
-3
# floor and truncation
import math
a = 33
b = 16
print(a/b)
print(a//b)
print(math.floor(a/b))
print(math.trunc(a/b)) # 2
2.0625
2
2
2
# floor and truncation
import math
a = -33
b = 16
print(a/b)
print(a//b)
print(math.floor(a/b)) # -3
print(math.trunc(a/b)) # -2
-2.0625
-3
-3
-2
# mod --> the equation: a = b* (a // b) + (a % b)
import math
a = 13
b = 4
print(f'{a}/{b} = {a / b}')
print(f'{a}//{b} = {a // b}')
print(f'{a}%{b} = {a % b}')
print('_'*50)
print(a == b * (a//b) + (a%b)) # Equation satisfied
13/4 = 3.25
13//4 = 3
13%4 = 1
__________________________________________________
True
# mod --> the equation: a = b* (a // b) + (a % b)
import math
a = -13
b = 4
print(f'{a}/{b} = {a / b}')
print(f'{a}//{b} = {a // b}')
print(f'{a}%{b} = {a % b}')
print('_'*50)
print(a == b * (a//b) + (a % b)) # Equation satisfied
-13/4 = -3.25
-13//4 = -4
-13%4 = 3
__________________________________________________
True
# mod --> the equation: a = b* (a // b) + (a % b)
import math
a = -13
b = -4
print(f'{a}/{b} = {a / b}')
print(f'{a}//{b} = {a // b}')
print(f'{a}%{b} = {a % b}')
print('_'*50)
print(a == b * (a//b) + (a % b)) # Equation satisfied
-13/-4 = 3.25
-13//-4 = 3
-13%-4 = -1
__________________________________________________
True
Integers: Constructors and Bases - Lecture
- The int class provides multiple constructors
- With one numerical parameter
- a = int(10), b = int(-10) → but we normally use the literal expression instead (a = 10)
- a = int(10.9), b = int(-10.9) → Result: Truncated (a = 10, b = 10)
- a = int(True), b = int(False) → (a = 1, b = 0)
- With strings that can be parsed to a number
- With strings that has an optional second parameter: base (2 <= base <= 36) → 0~9, A~Z = 10 + 26 = 36
- a = int(“1010”, base=2) or a = int(“1010”, 2) → a = 10
- a = int(“A12F”, base=16) → a = 41263
- Reverse Process: changing an integer from base 10 to another base
- bin(10) → ‘0b1010’
- oct(10) → ‘0o12’
- hex(10) → ‘0xa’
- a = 0b1010, b = 0o12, c = 0xA → (a = 10, b = 10, c = 10)
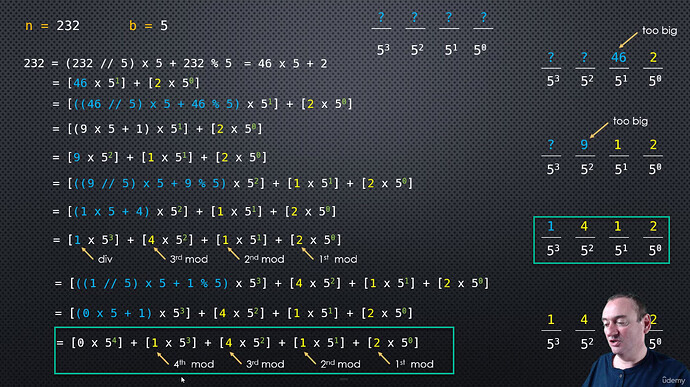
# Base 5
n = 232
b = 5
if b < 2:
raise ValueError('Base b must be >= 2')
if n < 0:
raise ValueError('Number n must be >= 0')
if n == 0:
print("The answer is 0")
digits = []
while n > 0:
m = n % b
n = n // b
digits.insert(0, m)
print(digits)
[1, 4, 1, 2]
# Base 16 with encoding
n = 1485 # number
b = 16 # Base
digits = []
while n > 0:
m = n % b
n = n // b
digits.insert(0, m)
print(digits)
# Start Encoding
map = '0123456789ABCDEF'
# encoding code 1 --> less efficient
encoding1 = ''
for d in digits:
encoding1 += map[d]
print(encoding1)
# encoding code 2 --> better (Use list comprehension)
encoding2 = ''.join([map[d] for d in digits])
print(encoding2)
[5, 12, 13]
5CD
5CD
Integers: Constructors and Bases - Coding
print(type(10))
print("_"*50)
print(int()) # default is 0
print(int(10.5))
print(int(10.999999))
print("_"*50)
print(int(True),"-" ,int(False))
<class 'int'>
__________________________________________________
0
10
10
__________________________________________________
1 - 0
import fractions
a = fractions.Fraction(22, 7)
print(a)
print("_"*50)
print(float(a))
22/7
__________________________________________________
3.142857142857143
print(int("12345"))
print("_"*50)
print(int("101", 2)) # 101 in base 2 --> 5 in base 10
print(int("FF", 16)) # FF in base 16 --> 255 in base 10
12345
__________________________________________________
5
255
print(int('A', 11))
print(int('B', 11))
10
---------------------------------------------------------------------------
ValueError Traceback (most recent call last)
c:\Users\joe.hu\Desktop\PyCode\DeepDive\Part 1\Section 04 - Numeric Types\S29-35.ipynb Cell 21 line 2
print(int('B', 11))
ValueError: invalid literal for int() with base 11: 'B'
# Base 10 --> Base 2
print(bin(10))
print(bin(5))
print("_"*50)
print(oct(10)) # Base 10 --> Base 8
print("_"*50)
print(hex(255)) # Base 10 --> Base 16
0b1010
0b101
__________________________________________________
0o12
__________________________________________________
0xff
# prefix: 0b --> base 2, 0o --> base 8, 0x --> base 16
print(int(0b101))
print(int(0o12))
print(int(0xff))
5
10
255
def from_base10(n, b):
if b < 2:
raise ValueError("Base b must >= 2")
if n < 0:
raise ValueError("Number n must be >= 0")
if n == 0:
return [0]
digits = []
while n > 0:
m, n = n % b, n // b # use tuple notation, alternatively n, m = divmod(n, b)
digits.insert(0, m)
return(digits)
def encode(digits, digit_map):
if max(digits) >= len(digit_map):
raise ValueError('digit_map is not long enough')
else:
return ''.join([digit_map[d] for d in digits]) # list comprehension
print(from_base10(10, 2))
print(from_base10(255, 16))
print("-"*20 + " Encoded " + "-"*20)
print(encode(from_base10(255, 16),'0123456789ABCDEF'))
[1, 0, 1, 0]
[15, 15]
-------------------- Encoded --------------------
FF
# dealing with negative number
def rebase_from10(number, base):
digit_map = '0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ'
if base < 2 or base > 36:
raise ValueError("Base must >= 2 or <= 36")
sign = -1 if number < 0 else 1
number *= sign
digits = from_base10(number, base)
encoding = encode(digits, digit_map)
if sign == -1:
encoding = '-' + encoding
return encoding
print(rebase_from10(10, 2))
print(int(rebase_from10(10, 2), base=2))
print(rebase_from10(-10, 2))
print(int(rebase_from10(-10, 2), base=2))
print('_'*50)
print(rebase_from10(3451, 16))
print(int(rebase_from10(3451, 16), base=16))
print(rebase_from10(-3451, 16))
print(int(rebase_from10(-3451, 16), base=16))
1010
10
-1010
-10
__________________________________________________
D7B
3451
-D7B
-3451
Rational Numbers - Lecture
- Rational numbers are fractions of integer numbers
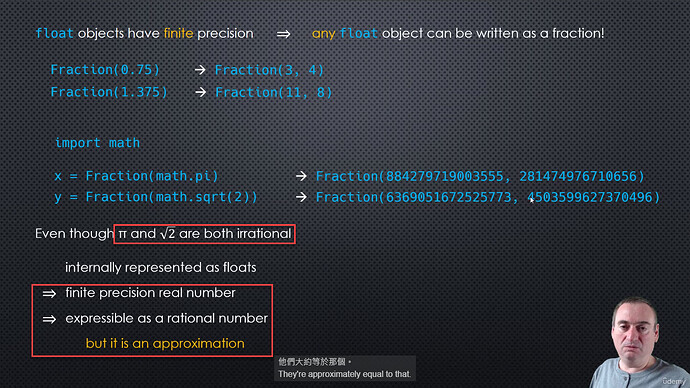
- Any real number with a finite number of digits after the decimal point is also a rational number
- Example of irrational number => square root of 2, Pi … etc.
- Can be represented in Python using the Fraction class in the fractions module
- Constructors
- Fraction(numerator=0, denominator=1) 未提供參數時,預設分子為 0,分母為 1
- Fraction(other_fraction)
- Fraction(float)
- Fraction(decimal)
- Fraction(string) => Fraction(‘10’), Fraction(‘0.125’), Fraction(‘22/7’)
Rational Numbers - Coding
from fractions import Fraction
# - help(Fraction)
# Fraction(1) => Fraction(1, 1)
print(Fraction(numerator=2, denominator=1))
print(Fraction(denominator=1, numerator=2))
print('_'*50)
print(Fraction(3, 4)) # three divided by four
print(Fraction(22, 7))
print(Fraction(0.125)) # => Fraction(1, 8)
print('_'*50)
print(Fraction('0.125')) # string can also work
print(Fraction('22/7')) # string can also work
2
2
__________________________________________________
3/4
22/7
1/8
__________________________________________________
1/8
22/7
from fractions import Fraction
print(Fraction(6, 10)) # Factions are automatically reduced:(自動約分) => Fraction(3, 5)
print(Fraction(1, -4)) # with negative denominator => change to negative numinator Fraction(-1, 4)
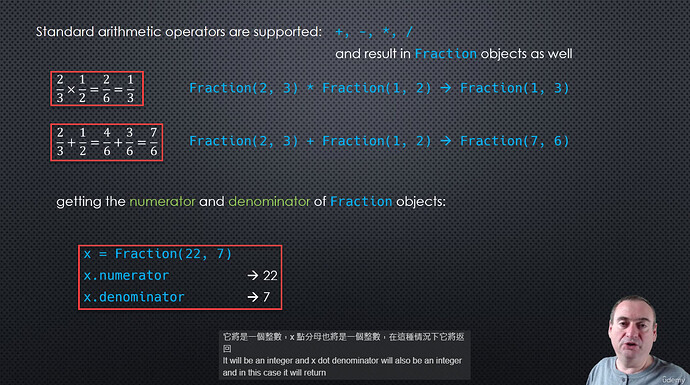
x = Fraction(1, -4)
print(x.numerator)
print(x.denominator)
print('_'*50)
x = Fraction(2, 3)
y = Fraction(3, 4)
print(x + y) # 自動擴分 => Fraction(17, 12)
print(x * y) # 最後約分至最簡分數 => Fraction(1, 2)
print(x / y) # => Fraction(8, 9)
3/5
-1/4
-1
4
__________________________________________________
17/12
1/2
8/9
# irrational number - Pi and square root of 2
import math
print(Fraction(math.pi))
print(float(Fraction(math.pi))) # we can only get a finite representation
print('_'*50)
print(Fraction(math.pi).limit_denominator(10))
print(Fraction(math.pi).limit_denominator(100))
print(Fraction(math.pi).limit_denominator(500))
print(float(Fraction(math.pi).limit_denominator(500)))
print('_'*50)
print(Fraction(math.sqrt(2)))
print(float(Fraction(math.sqrt(2)))) # we can only get a finite representation
884279719003555/281474976710656
3.141592653589793
__________________________________________________
22/7
311/99
355/113
3.1415929203539825
__________________________________________________
6369051672525773/4503599627370496
1.4142135623730951
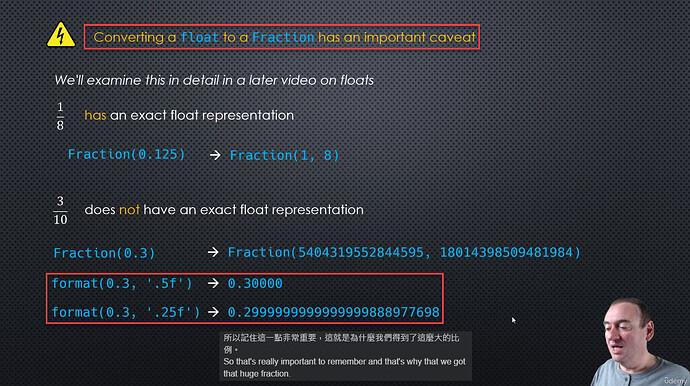
# not all floating point numbers can be represented precisely or exactly in a computer
print(Fraction(0.125))
print(Fraction(0.3))
print('_'*50)
print(format(0.3, '0.5f'))
print(format(0.3, '0.15f'))
print(format(0.3, '0.25f'))
1/8
5404319552844595/18014398509481984
__________________________________________________
0.30000
0.300000000000000
0.2999999999999999888977698